Tantangan AI: Generator Triple Pythagoras Primitif Intuitif

AI menampilkan kemampuan mempesona. AI tampak cerdas bahkan super cerdas. Sampai muncul istilah ASI: artificial super intelligence. Seberapa cerdaskah AI? Kita akan memberi tantangan AI berupa triple Pythogras. Hasilnya, kecerdasan AI sangat terbatas; jelas AI tidak super cerdas.

Triple Pythagoras memicu kreativitas sejak ribuan tahun yang lalu. Barangkali sudah berkembang puluhan sampai ratusan generator untuk menghasilkan triple Pythogoras; primitif mau pun tidak primitif. Tulisan ini akan mengembangkan generator Pythagoras versi paman APIQ yang lebih intuitif; lengkap untuk primitif dan tidak primitif.

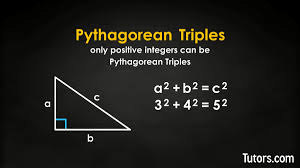
Anda lebih hebat dari AI ketika Anda menguasai triple Pythagoras APIQ. Karena AI (akal imitasi atau artificial intelligence) gagal menguasai triple Pythagoras. Bahkan Meta, Gemini, ChatGpt dan kawan-kawan sudah gagal di tahap-tahap awal triple Pythagoras. Tentu saja, Anda bisa membuat program komputer untuk menghitung triple. Tetapi program ini adalah karya Anda, karya manusia, bukan karya AI.

1. Generator Umum
2. Generator Ganjil
3. Generator Genap
4. Generator Primitif Ganjil
5. Generator Primitif Genap
6. Diskusi

Contoh triple Pythagoras adalah: (3, 4, 5); (5, 12, 13); (7, 24, 25); (8, 15, 17).

Contoh tidak primitif adalah membuat kelipatan dari yang primitif: (6, 8, 10); (10, 24, 26); (14, 48, 50).

Tentu saja jumlah triple tidak primitif lebih banyak, lebih mudah ditemukan, dibanding triple primitif. Kita sedikit membedakan segitiga siku dengan segitiga Pythagoras. Segitiga siku berlaku rumus Pythagoras untuk bilangan real (bulat, pecahan, irasional dll). Sedangkan, segitiga Pythagoras hanya untuk bilangan asli, bilangan bulat positif. Triple Pythagoras, yang merupakan sisi-sisi segitiga Pythagoras, menjadi menarik dan indah karena terbatas hanya boleh bilangan asli saja.

1. Generator Umum

Generator umum berhasil menghasilkan triple Pythagoras secara lengkap: primitif dan tidak primitif.

(a^2)/n = 2b + n

Hasil triple adalah (a, b, c) = (a, b, [b+n])

n = 1, 2, 3, …

Karena n lengkap untuk seluruh bilangan asli maka generator adalah lengkap untuk seluruh triple yang mungkin.

2. Generator Ganjil

Generator ganjil adalah untuk a = 3, 5, 7, 9…

Untuk n = 1, menghasilkan triple primitif seluruhnya:

a^2 = 2b + 1

Contoh:

a = 3; maka

3^2 = 2b + 1
9 = 2b + 1 = 4 + 5 ==> (3, 4, 5).

a = 5 maka

5^2 = 2b + 1
25 = 12 + 13 ==> (5, 12, 13).

Anda bisa mencoba dengan a berupa bilangan ganjil yang besar,

a = 53 maka

53^2 = 2b + 1
2809 = 1404 + 1405 ==> (53, 1404, 1405).

Anda lebih hebat dari AI karena bisa bertanya kepada AI: sebutkan semua triple Pythagoras dengan salah satu sisinya 53.

AI akan gagal menemukan (53, 1404, 1405).

Jawaban Gemini: “Mencari semua triple Pythagoras dengan salah satu sisi 53 membutuhkan pendekatan komputasi. Meskipun tidak ada rumus sederhana, dengan menggunakan program komputer, kita dapat menemukan semua solusi yang mungkin.”

Memang manusia bisa lebih kreatif dari AI.

3. Generator Genap

Generator genap adalah untuk a = 4, 6, 8, …

Untuk n = 2, generator menghasilkan primitif jika a = 4k dengan k = 1, 2, 3,..

(a^2)/2 = 2b + 2
(a/2)^2 = b + 1

Contoh:

a = 4

(4/2)^2 = b + 1
4 = b + 1
b = 3; c = 5 ==> (4, 3, 5).

a = 8

(8/2)^2 = b + 1
16 = b + 1
b = 15; c = 17 ==> (8, 15, 17)

Untuk menantang AI anda bisa memilih a yang cukup besar.

a = 104

(104/2)^2 = b + 1
2704 = b + 1
b = 2703; c = 2705 ==> (104, 2703, 2705).

Hebat, manusia memang bisa lebih kreatif dari AI.

Istilah ganjil dan genap bisa, lentur, kita terapkan terhadap n mau pun a.

4. Generator Primitif Ganjil

Primitif kita peroleh ketika n = p^2 yaitu kuadrat dari bilangan prima.

Untuk n = p atau n = p*q*r… berupa perkalian dari bilangan-bilangan prima maka akan menghasilkan triple yang tidak primitif. Kita perlu fokus, umumnya, untuk menghasilkan primitif.

Contoh:

n = p^2 = 3^2 = 9

(a^2)/9 = 2b + 9

misal a = 15

(15^2)/9 = 2b + 9
25 = 2b +9
b = 8; c = 17 ==> (15, 8, 17).

Untuk menantang AI kita perlu memilih a yang cukup besar.

a = 3*41 = 123

(123^2)/9 = 2b + 9
1681 = 2b + 9
b = 836; c = 845 ==> (123, 836, 845).

5. Generator Primitif Genap

Primitif kita peroleh ketika n = 2(p^2) yaitu berupa kuadrat bilangan prima yang kemudian dikalikan 2.

Contoh

n = 2(2^2) = 8

(a^2)/8 = 2b + 8
(a/4)^2 = b + 4

Misal a = 20

(20/4)^2 = b + 4
25 = b + 4
b = 21; c = 29 ==> (20, 21, 29).

Untuk menantang AI kita memilih a agak besar.

a = 4*41 = 164

(164/4)^2 = b + 4
1681 = b + 4
b = 1677; c = 1685 ==> (164, 1677, 1685).

Apa maksud generator APIQ adalah intuitif?

Intuitif adalah kita bisa menggunakan generator APIQ hanya bermodal pensil dan kertas. Bahkan dalam contoh di atas, saya hanya memanfaatkan imajinasi tanpa pensil dan kertas untuk perhitungan; tentu tanpa kalkulator atau pun komputer.

Contoh terakhir, yang terbesar, hanya 41 x 41 = 1681. Anda tentu bisa menghitungnya, 41 x 41, dengan pensil dan kertas. Bila kita pakai metode Bintang APIQ memang bisa menghitung dengan imajinasi dalam mental saja.

Sementara itu, ketika orang lain ingin verifikasi apakah (164, 1677, 1685) adalah triple Pythagoras primitif, mereka justru membutuhkan kalkulator atau komputer. AI tampaknya tidak bisa membantu untuk verifikasi ini.

Berikut jawaban Gemini:

“Memeriksa Teorema Pythagoras:

• a² + b² = c²
• 164² + 1677² = 1685²
• 26896 + 2815529 = 2839825
• 2842425 = 2839825

Ternyata, persamaan di atas tidak benar. Ini berarti bahwa (164, 1677, 1685) bukan triple Pythagoras.”

Gemini salah dalam melakukan perhitungan dan, akibatnya, salah mengambil kesimpulan di atas.

6. Diskusi

Bagaimana menurut Anda?

Saya menduga bilangan prima p = 1, 2, 3, 5, 7… adalah mirip bilangan prima di jaman kuno; yaitu 1 termasuk bilangan prima.

Konsekuensinya, triple primitif menjadi lebih konsisten.

Primitif ganjil maka n = p^2 dengan p = 1, 2, 3, 5,…

Untuk p = 1 primitif ketika a = 1*(2k + 1) dengan k = 1, 2, 3…
Untuk p = p primitif ketika a = p*q dengan q = 3, 5, 7, 11…

Primitif genap maka n = 2p^2 dengan p = 1, 2, 3, 5, …

Untuk p = 1 primitif ketika a = 2*2k
Untuk p = p primitif ketika a = 2p*q

Waspada AI

Kembali ke AI yang mengalami kesulitan menghadapi triple Pythagoras karena, diduga, kurang data latihan. ChatGPT mampu membuat kode, misal dengan Python. Ketika kode ini valid maka AI mampu menghitung triple. Dalam kasus ini, bukan AI yang menghitung triple tetapi kode yang menghitung triple. Jadi, tugas kita adalah belajar kode agar mampu menguji apakah kode dari AI valid?

Lalu, mengapa pakai AI jika kode masih harus kita uji lagi? Lumayan, AI mampu membantu kita menulis kode. Bayangkan jika kode tersebut terdiri 2025 baris. Betapa berat menuliskannya. AI akan menulis kode tersebut kemudian kita tanggung jawab untuk menguji dan koreksi. Bagaimana pun, AI belajar dari kode yang sudah dibuat manusia sebelumnya. Fenomena ini menjadi problem AI yang perlu diwaspadai.

Kembali kepada AI yang mengandalkan LLM memang sulit menangani triple Pythagoras. Sebenarnya, AI juga sulit menangani semua bahasa sehari-hari. Ketika Anda bertanya ke AI: siapa saja anak kandung dari presiden Indonesia? AI sulit menjawabnya. Hanya saja, kita toleran terhadap jawaban AI. Ketika sebagian jawaban valid dan sebagian lain ngawur maka kita toleran. Lebih jauh, jawaban yang valid itu sendiri adalah sekedar kebetulan.

Jadi, kita perlu waspada dengan AI.

Bagaimana menurut Anda?