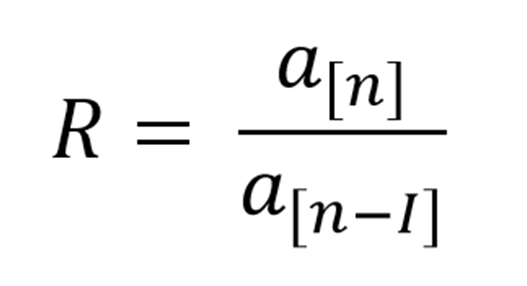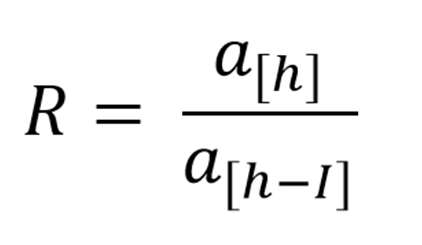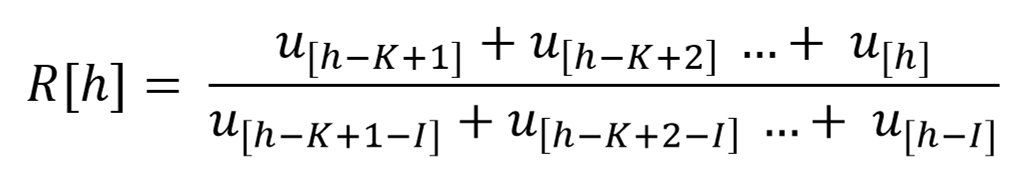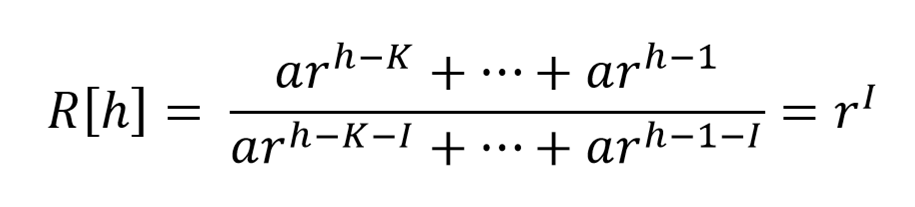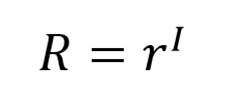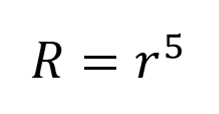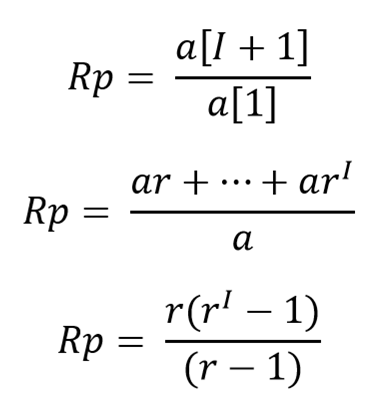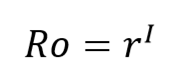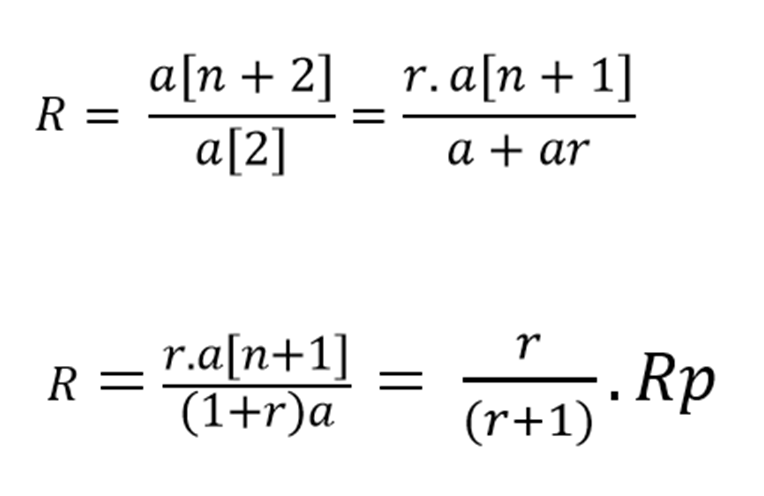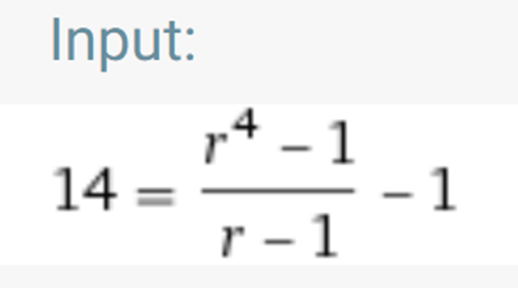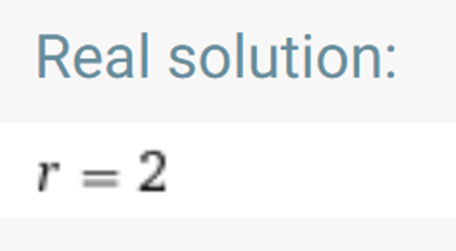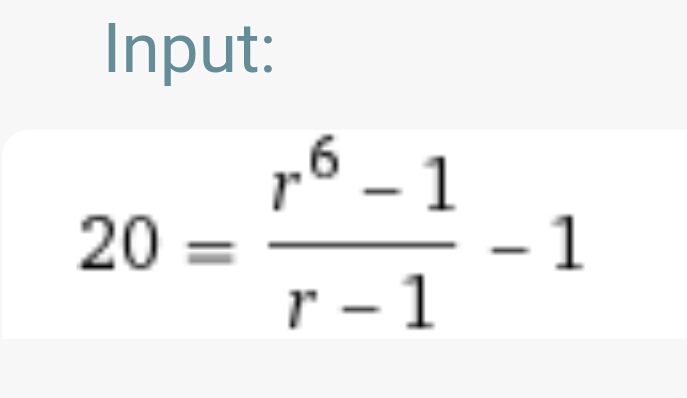Bawa Kebaikan ke Manusia & Manusia ke Kebaikan

Metode Estimasi Angka Reproduksi dengan Geometric Mean of Ratio

Abstrak

Metode estimasi nilai angka reproduksi R menjadi sangat penting karena menentukan apakah suatu wabah masih akan terus berkembang atau akan mereda. Berbagai metode estimasi telah dikembangkan baik menggunakan kalkulasi sederhana, kalkulus, statistik, dan lain-lain. Kajian ini bermaksud mengusulkan satu metode baru yaitu geometric mean of ratio – GMR. Dengan GMR, estimasi mudah dilakukan cukup dengan perangkat kalkulator atau komputer sederhana, periode sampling fleksibel sehingga memungkinkan didapat data nilai R secara realtime. GMR dapat mengestimasi nilai R baik Rt atau Re dan Ro.

Pendahuluan

Tinjauan metode terdahulu

Berikut sebagian metode estimasi R yang sudah dikenal. Metode kalkulasi sederhana mengestimasi R dengan asumsi R berbanding lurus dengan besarnya populasi yang rawan terinfeksi dan kecepatan transmisi virus. Tetapi berbanding terbalik dengan kecepatan suatu kasus selesai – karena sembuh lalu imun atau atau karena meninggal.

Metode kalkulus, salah satunya adalah model SIR. Metode ini mendekati nilai R dengan menyusun beberapa sistem persamaan diferensial lalu memecahkannya. Guna menyusun sistem persamaan diperlukan berbagai macam asumsi termasuk periode inkubasi, recovered, periode berlipat dua, dan lain-lain.

Kajian ini mengusulkan metode geometric mean of ratio yang memanfaatkan data-data lapangan khususnya data kasus baru, kasus sembuh, dan kasus meninggal.

Metodologi

Metode GMR memanfaatkan laporan data lapangan untuk mendapatkan data total kasus aktif dan memanfaatkan laporan dari bidang kesehatan yang mengestimasi periode inkubasi suatu virus.

Berikutnya menyusun model matematika untuk estimasi R di mana kita mengasumsikan bahwa virus berkembang mengikuti deret geometri secara natural. Asumsi ini sesuai dengan sifat replikasi virus dan wabah pada umumnya.

Pembuktian matematika untuk meyakinkan bahwa perhitungan GMR adalah valid. GMR dapat kita gunakan untuk menghitung Rt ketika waktu sudah cukup lama, data stabil, secara langsung. Sedangkan untuk menghitung Ro dilakukan ketika wabah baru berkembang dengan memecahkan sistem persamaan R.

Selanjutnya penerapan GMR ke sistem kehidupan nyata mempertimbangkan proses stokastik. Di sini kita menerapkan berbagai macam metode statistik untuk menetapkan mean, median serta confidence interval.

Pengumpulan Data

Data yang perlu dikumpulkan adalah data penambahan kasus baru harian, sembuh harian, dan meninggal harian. Data ini bisa kita buat sendiri. Atau dalam kasus covid-19 kita dapat memanfaatkan data yang disediakan oleh gugus tugas secara resmi.

Selanjutkan data hasil penelitian yang menunjukkan periode inkubasi. Untuk kasus covid-19, periode inkubasi kisaran 2 – 14 hari dengan mean 5,2 hari dan ci 95%. Beberapa peneliti mungkin saja menghasilkan laporan yang berbeda.

Data kasus harian baru kita misalkan sebagai u[h].

u[h] = banyaknya kasus baru pada hari h

Banyak kasus aktif kita misalkan a[h].

a[h] = banyaknya kasus aktif pada hari h.

Maka angka reproduksi R dapat kita hitung,

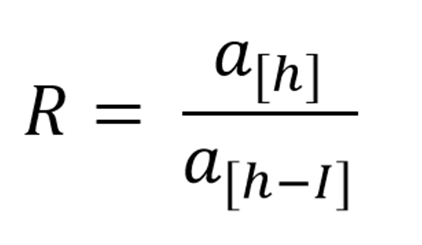
untuk h > 2I.

I = periode inkubasi, misal dalam kasus covid-19 kita ambil 5 hari.

Pembuktikan Matematika

Banyaknya total kasus aktif, a[h], pada hari h adalah banyaknya seluruh kasus dikurangi dengan banyaknya kasus yang sudah “keluar” – karena sudah sembuh atau karena meninggal.

Untuk pembuktian, kita akan meninjau kasus deterministik di mana periode inkubasi tepat I hari dan kasus keluar (sembuh atau meninggal) tepat K hari setelah inkubasi.

Maka

a[h] = S[h] – S[h-K]

S[h] = u[1] + u[2] + … + u[h]

S[h] menyatakan banyaknya jumlah seluruh kasus dari hari 1 sampai hari h. Dan r menyatakan rasio geometri harian.

Dengan cara yang sama,

a[h-I] = S[h-I] – S[h-I-K]

Bagaimana pun a[h] dapat kita pandang sebagai suatu barisan geometri sesuai sifat replikasi virus atau wabah.

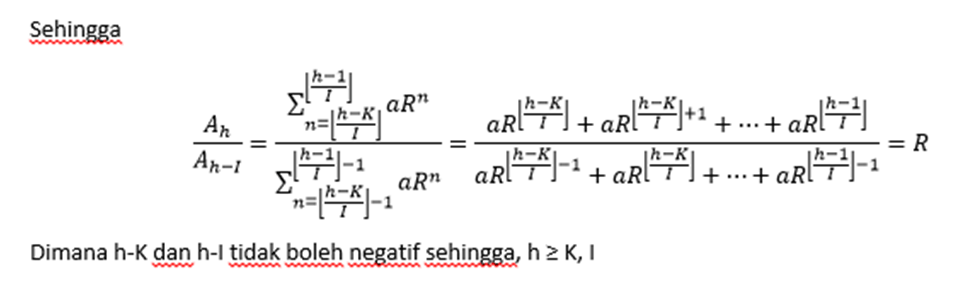
Maka

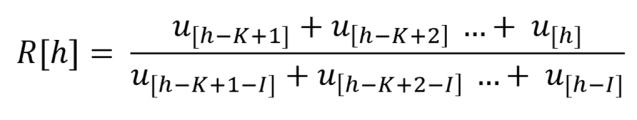
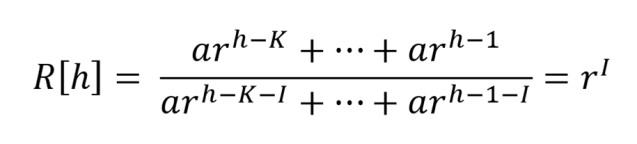
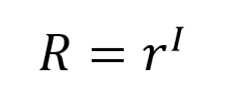
Terbukti perbandingan total kasus aktif menunjukkan angka pertumbuhan. Karena laporan kasus baru terdeteksi, umumnya, pada periode inkubasi maka kita mengambil periode inkubasi sebagai acuan.

Kita dapat menulis ulang,

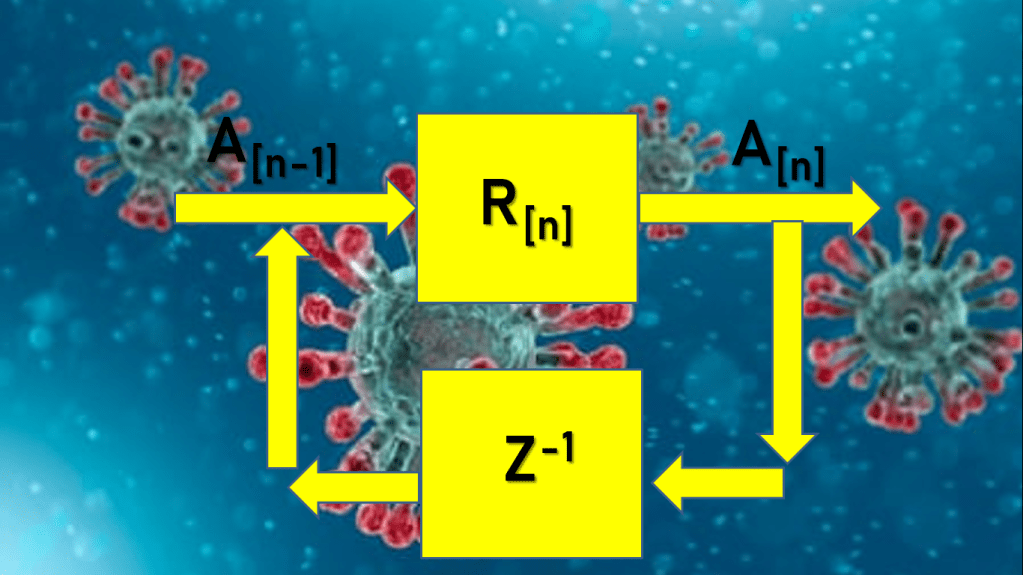
A[n] = R*A[n-1]

Di mana sistem dinamik ini menunjukkan A[n] divergen, menuju tak hingga, bila R > 1. Sesuai dengan definisi bahwa wabah terus berkembang jika R > 1.

Dan A[n] menuju 0 bila R < 1. Sesuai dengan definisi bahwa wabah akan selesai bila R < 1.

Menentukan nilai Ro

Nilai Ro kita estimasi ketika h < 2I dimana kita mendapatkan nilai R transien.

Dapat kita tunjukkan bahwa nilai R maksimum = Rp = R puncak.

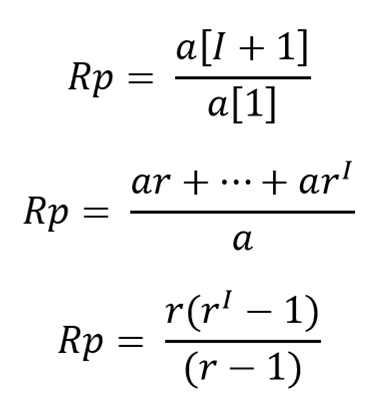
Karena data pertama, paling awal, tersedia adalah a[1] maka kita definisikan

a[h] = a[1]

untuk semua h < 1.

Agar lebih mudah analisis kita juga dapat mendefinisikan a[h] = 0 untuk semua h < 1.

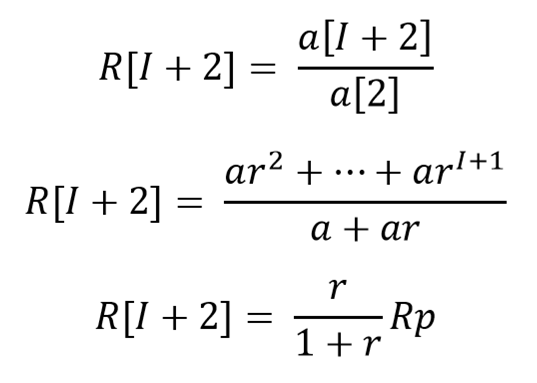
Terbukti bahwa Rp adalah R maksimal untuk I < h < 2I. Sedangkan untuk h < I maka bagian pembilang menjadi lebih kecil karena banyaknya suku kurang dari I suku dan penyebut tetap a[1]. Atau kita dapat mendefinisikan R = 1 untuk h < 1.

Yang menarik adalah untuk h = 2I maka dua cara menghitung R di atas – R transien dan R stabil – memberikan hasil R yang sama. Sehingga R dapat kita pandang sebagai fungsi kontinyu untuk h > 0.

Pengembangan Sistem Dinamik R

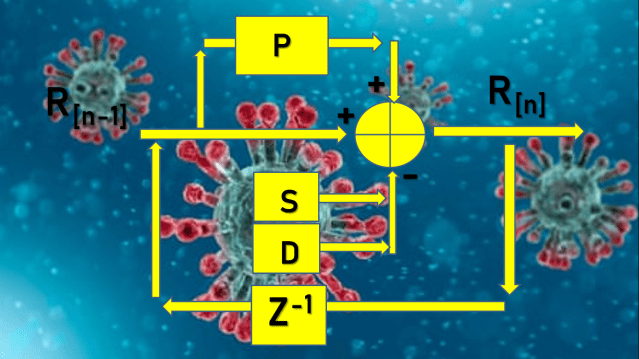
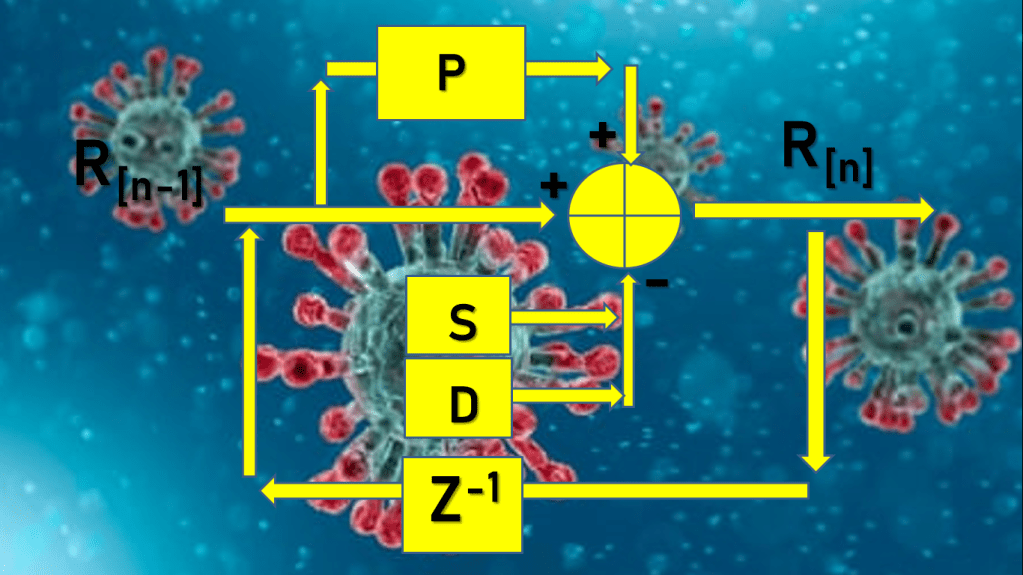
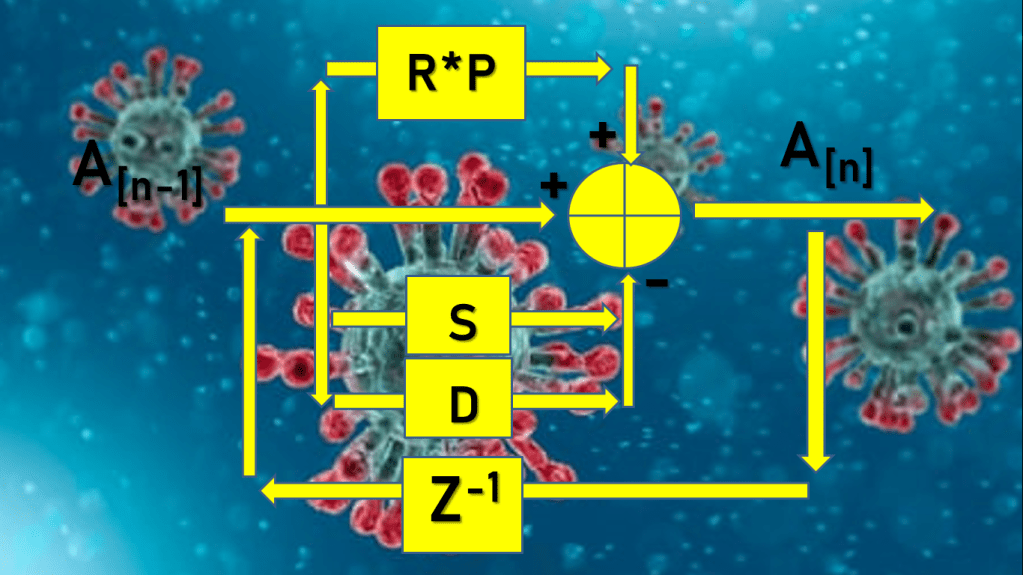
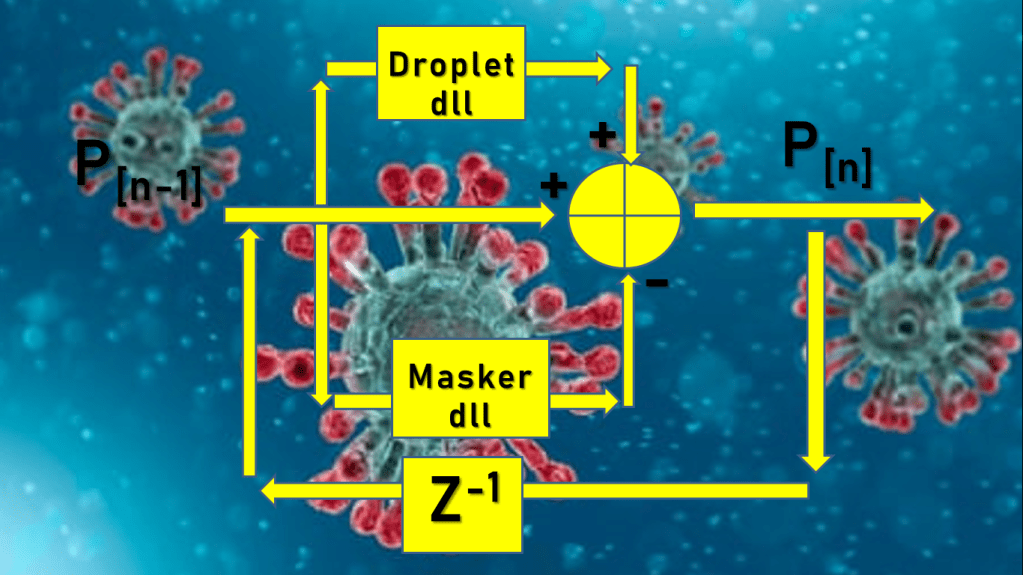
Di satu sisi kita membutuhkan cara efektif untuk estimasi R. Di sisi lain kita juga memerlukan suatu cara untuk mengendalikan nilai R. Maka saya menyusun sistem dinamik R sebagai berikut ini.

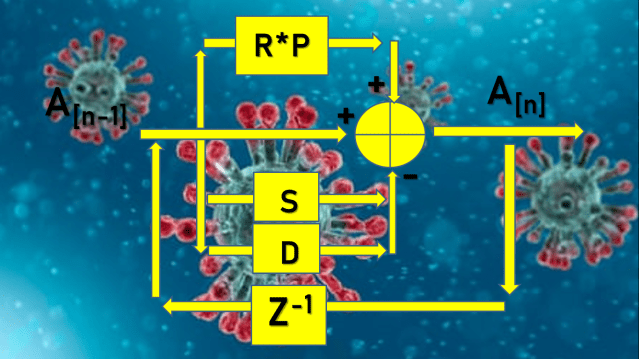
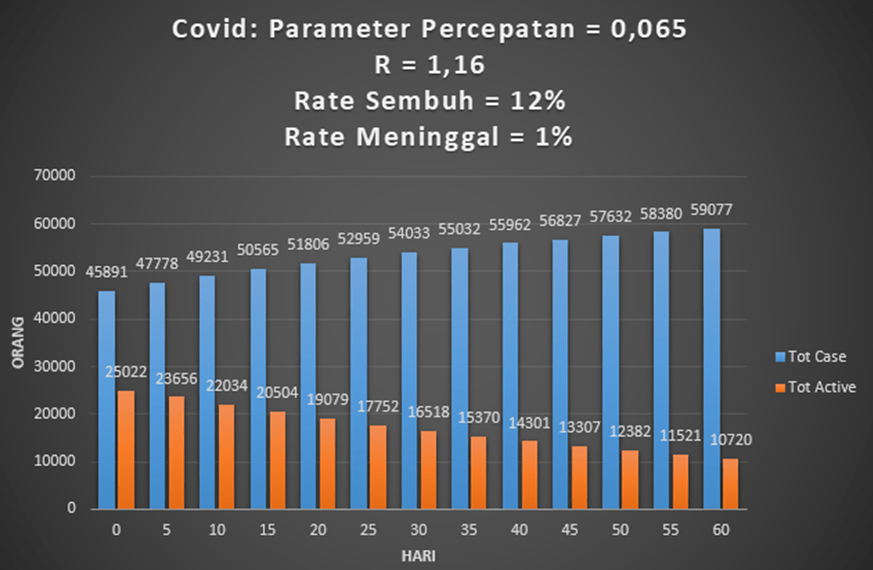
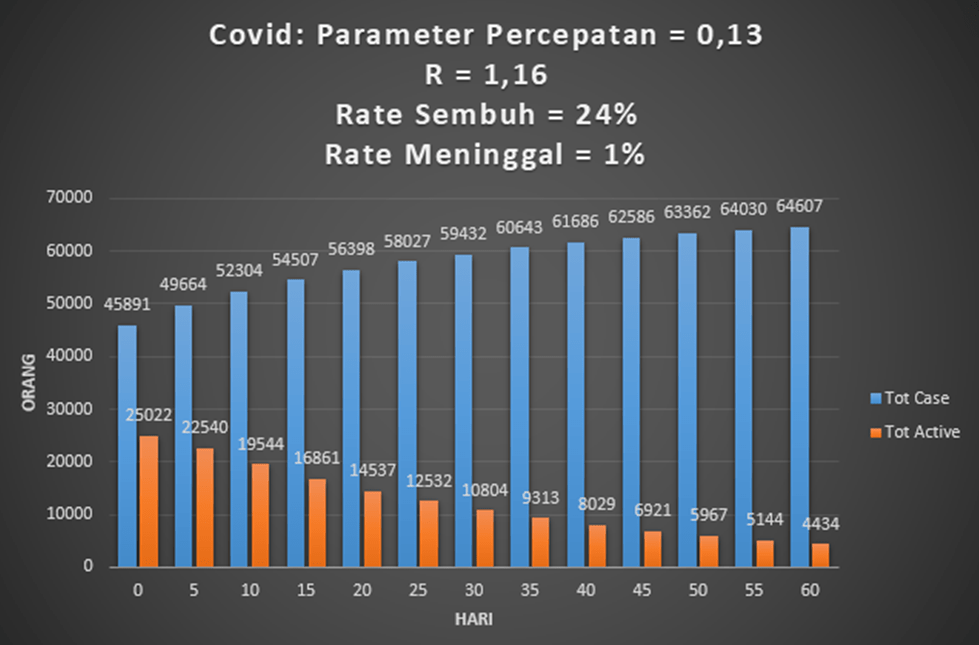
S = rate sembuh, diperoleh dari data lapangan
D = rate death, diperoleh dari data lapangan
P = paramater perilaku diperoleh dari perhitungan hari h-1

Metode Statistik

Kita memerlukan metode statistik di lapangan. Misalnya, hasil penelitian yang menyebutkan periode inkubasi I = 5,2 hari adalah tidak eksak. Melainkan merupakan mean atau median dengan confidence interval 95%.

Mempertimbangkan 5,2 hari adalah pecahan kita dapat membulatkan menjadi I = 5 hari. Hal ini lebih sesuai dengan ritme kehidupan manusia. Termasuk pencatatan dan pelaporan data yang kita perlukan.

Untuk mejaga kesinambungan hasil perhitungan dengan periode sebelumnya maka kita dapat menggunakan geometric mean rentang tiga hari terakhir. Maka nilai R yang akan kita sajikan menjadi,

R = (R[n]*R[n-1]*R[n-2])^{1/3)

Penggunaan geometric mean ini memberi informasi penting tentang histori. Misal di masa lalu nilai R > 1 kemudian jumlah total aktif a[h] konstan dalam waktu yang lama maka R tetap lebih dari 1 meski mendekati 1. Bila tidak memakai geometric mean maka R = 1, tepat.

Demikian pula jika R < 1 di masa lalu kemudian total kasus aktif a[h] konstan dalam rentang waktu yang lama maka tetap R < 1, meski makin dekat dengan 1.

Koreksi pembulatan periode inkubasi

Akibat kita membulatkan I ke bilangan bulat terdekat maka kita perlu melakukan koreksi pada hasil akhir. Terdapat tiga cara untuk melakukan koreksi.

Pertama, tidak dilakukan koreksi apa pun. Pertimbangannya adalah kita hanya memerlukan informasi R apakah lebih besar atau lebih kecil dari 1. Dan informasi ini sudah kita peroleh dengan baik.

Kedua, koreksi dengan cara mengalikan hasil akhir dengan faktor (5.2)/5 = 104%. Koreksi ini bersifat pesimis karena hasil koreksi R akan lebih besar 4% dari estimasi R semula. Tetapi hasil koreksi ini penting di lapangan karena menjadikan berbagai pihak lebih waspada.

Ketiga, koreksi proporsional. Dengan cara memangkatkan hasil estimasi R dengan pangkat (5,2)/5 = 1,04. Hasil koreksi ini memperkuat nilai R semula menjadi lebih lebar dari R = 1. Metode koreksi ketiga ini adalah yang paling konsisten secara matematis.

Perhitungan confidence interval

Menghitung confidence interval dapat kita lakukan dengan dua cara. Pertama langsung memanfaat ci yang tersedia dari sumber data inkubasi. Misal I = 5,2 hari dengan ci = 95% maka hasil estimasi R memiliki ci = 95% juga.

Hal ini karena kita memanfaatkan satu besaran yang berhubungan dengan I yaitu a[h-I] sebagai pembagi terhadap a[h].

Batas atas dan batas bawah konsisten mengikuti batas atas dan batas bawah dari mean periode inkubasi. Perlu dicatat bahwa ketika R < 1 kadang kita perlu menukar posisi batas atas dan batas bawah.

Cara kedua menghitung ci adalah dengan menghitung berbagai macam R dengan periode inkubasi yang beragam. Lalu mengolah hasil perhitungan R ini untuk mendapatkan mean atau median lengkap dengan confidence interval yang diperlukan.

Misal untuk kasus covid-19 kita dapat menghitung R untuk asumsi periode inkubasi 1 hari sampai dengan periode inkubasi 14 hari. Maka kita peroleh dara R sebanyak 14 buah data. Dari data ini kita hitung mean atau median lengkap dengan confidence interval.

Asumsi periode 7 hari

Jika tidak tersedia data dari pihak lain tentang periode inkubasi maka kita dapat melakukan estimasi periode sebagai I dan memanfaatkan periode kerja manusia membentuk ritme 7 harian.

Misal untuk kasus covid-19 kita estimasi sendiri I = 4 hari, karena tidak tersedia data dari pihak lain. Selanjutnya kita akan menghitung R[sementara] berikut,

R[s] = a[h]/a[h-7]

dan

R = R[s])^(I/7) = R[s]^(4/7)

Hasil estimasi R ini tetap konsisten. Bahkan lebih sesuai dengan ritme kerja manusia 7 harian.

Data Realtime

Kita memerlukan data realtime R untuk dimanfaatkan oleh banyak pihak menentukan respon guna mengendalikan suatu wabah.

Dalam contoh kasus covid-19 kita melakukan sampling data setiap 1 hari. Rentang waktu 1 hari kadang dirasa terlalu lama untuk dari sisi praktis. Maka kita dapat melakukan sampling lebih sering misalnya tiap 1 jam. Yakni terjadi 24 sampling dalam 1 harinya.

Tentu saja sampling tiap 1 jam tetap konsisten dengan perhitungan di atas. Poin terpenting adalah konsisten membandingkan a[h] dengan a[h-I]. Yaitu, sebagai contoh, membandingkan hasil sampling pukul 09.00 hari Senin dengan hasil sampling pukul 09.00 hari Rabu sebelumnya.

Periode sampling yang lebih pendek menghasilkan grafik R yang lebih halus.

Simulasi

Bagian awal simulasi kita akan menghitung nilai Ro dengan data-data simulasi yang tersedia untuk negara Indonesia secara nasional. Bagian selanjutnya kita akan simulasi menghitung nilai R efektif Indonesia dan beberapa wilayah.

Ro Indonesia

Data yang resmi dipublikasikan di Indonesia pada awal-awal covid-19 dapat kita lihat di bagian bawah ini.

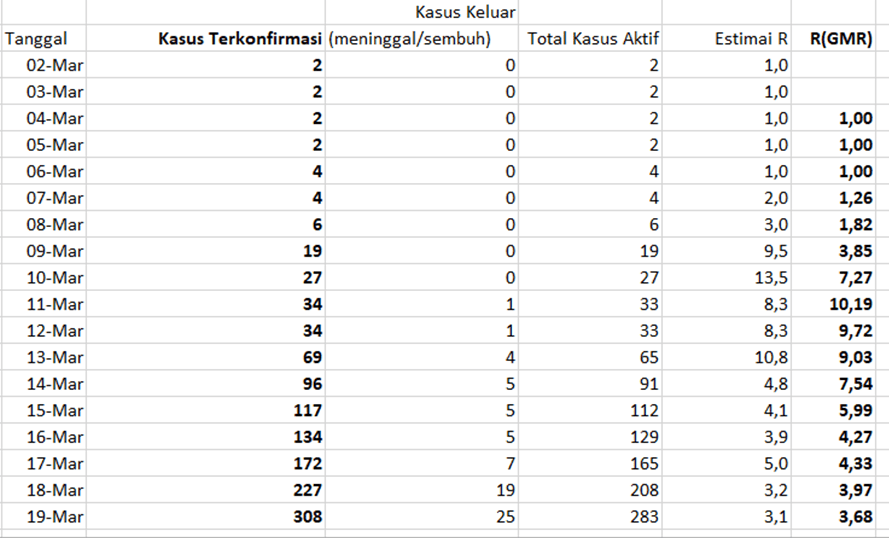
Pada masa-masa awal ini, kasus keluar utamanya dikarenakan meninggal. Kasus keluar karena sembuh menunggu waktu realtif lebih lama. Dari data di atas kita estimasi nilai

R[h] = a[h]/a[h-5]

Kita peroleh grafik R sebagai berikut.

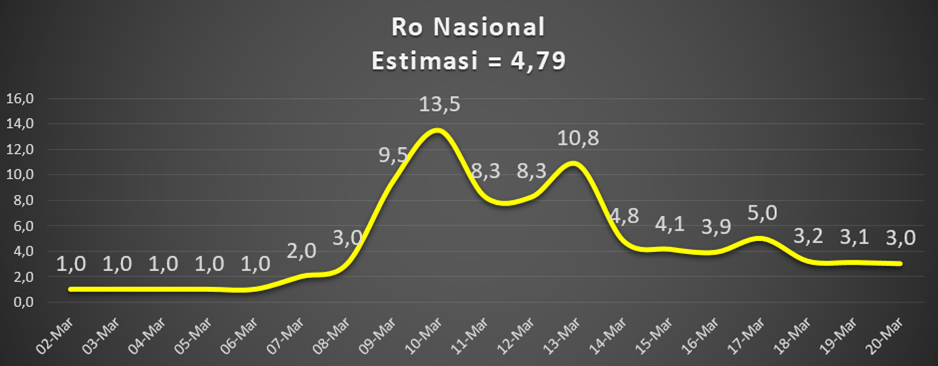
Selanjutnya kita akan memecahkan persamaan Rp = 13,5 untuk mendapatkan nilai r yang merupakan geometric mean of ratio harian. Kita memilih periode inkubasi I = 5 hari.

Kita peroleh r = 1,35

Maka Ro,

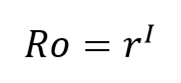
Ro = 4,51

Sedangkan bila kita menerapkan faktor koreksi dengan memangkatkan I = 5,2 maka kita peroleh Ro lebih besar.

Ro (Setelah koreksi) = 4,79

Nilai Ro ini penting ketika kita hendak menyusun strategi herd immunity di mana diperlukan minimal 1 – 1/Ro dari populasi harus imun. Baik imun karena sembuh dari infeksi atau vanksinasi. Untuk kasus Indonesia di atas maka batas minimal imun adalah,

1 – 1/Ro = 1 – 1/4,79 = 0,79 = 79%

Ditbutuhkan 79% populasi imun agar tercapai herd immunity.

R efektif Indonesia

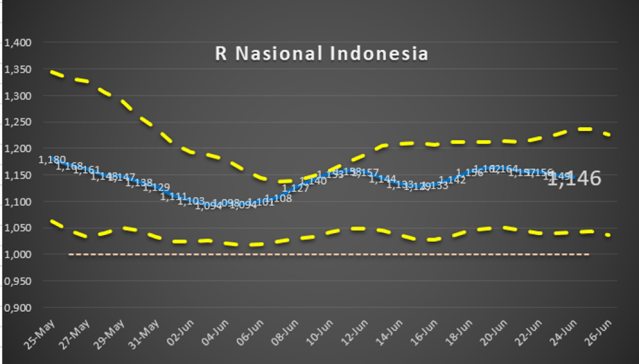
Berikutnya kita akan melakukan simulasi perhitungan R efektif untuk Indonesia. Kita mengacu data resmi yang diumumkan oleh gugus tugas melalui berbagai media.

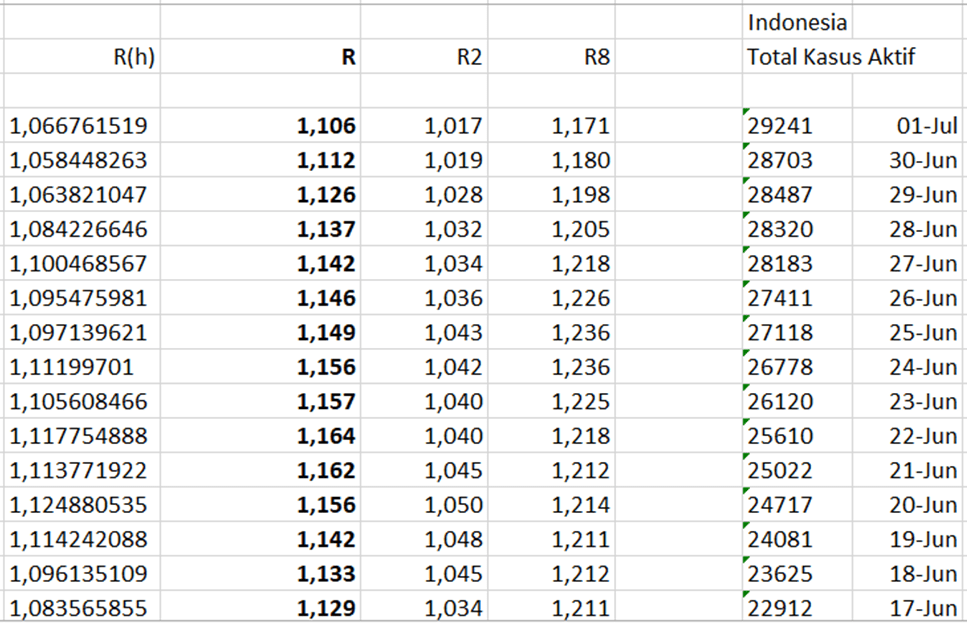
R[h] = a[h]/a[h-5]

R = geometric mean of R[h], R[h-1], R[h-2] dan faktor koreksi 1,04

R2 = batas bawah (garis putus bawah) = a[h]/a[h-2]

R8 = batas atas (garis putus atas)= a[h]/a[h-8]

Kita sajikan dalam bentuk grafik R Indonesia sebagai berikut.

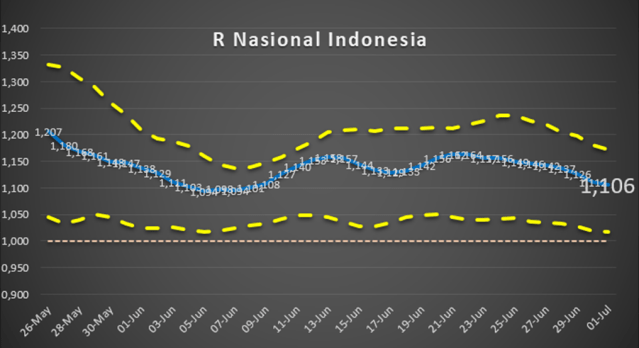
Kita lihat nilai R Indonesia sepanjang bulan Juni 2020 konsisten lebih dari 1. Di mana hal ini menunjukkan bahwa pandemi di Indonesia masih terus berkembang selama bulan Juni.

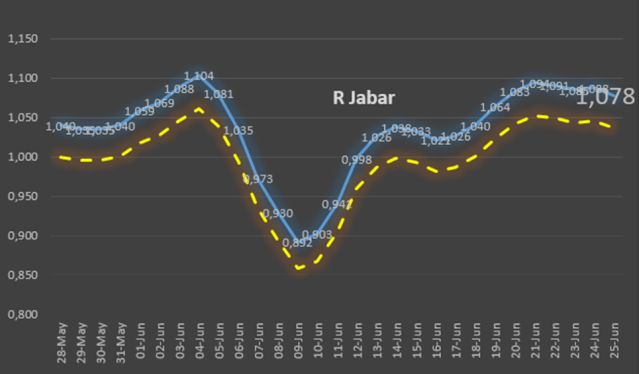
Hasil yang berbeda ketika kita simulasi menghitung nilai R dari Bali. Pada bulan Mei 2020, Bali sempat nilai R di bawah 1 cukup lama. Sedangkan di bulan Juni, nilai R Bali juga konsisten di atas 1. Hal ini menunjukkan nilai R dinamis berubah seiring waktu.

Hasil Kajian

Metode GMR untuk estimasi angka reproduksi terbukti efektif dan mudah dilakukan. Karena GMR hanya membutuhkan operasi hitung perbandingan dan eksponen maka bisa dilakukan hanya dengan komputer sederhana atau kalkulator.
Metode GMR mengacu hasil kajian statistik dari pihak lain, atau dilakukan kajian sendiri, untuk menentukan periode inkubasi maka confidence interval hasil estimasi GMR terkait dengan confidence interval dari data acuan.
Metode GMR, secara mendasar, melakukan operasi hitung terhadap data kasus total aktif. Maka akurasi data kasus total aktif menjadi sangat penting.
Karena hakikat nilai R tidak diketahui maka GMR hanya dapat melakukan estimasi. Pendekatan statistik menjadi penting. Menentukan mean atau median lengkap dengan confidence interval.
Pembuktian matematika menentukan nilai r, geometric mean of ratio harian, memudahkan kita menentukan nilai R efektif dan Ro.
Nilai R efektif dapat langsung dihitung dari formula R = a[h]/a[h-I] untuk besaran waktu h > 2I.
Sedangkan untuk h < 2I kita perlu memecahkan persamaan R puncak untuk mendapat nilai r kemudian menghitung Ro.
Untuk mendapatkan nilai R yang stabil dan terkait dengan histori maka disarankan untuk menghitung geometric mean dari R.
Faktor koreksi perlu diterapkan mengingat kegiatan manusia terbiasa periodik harian atau mingguan. Sementara pertumbungan virus tidak terikat periode yang sama.
Hasil simulasi menunjukkan nilai R dinamik bergerak naik turun. Maka perlu mempertimbangkan nilai R dalam rentang waktu yang cukup lama.
Hasil simulasi R untuk Indonesia menunjukkan angka konsisten di atas 1 maka perlu respon seluruh pihak terkait dengan lebih waspada.
Hasil simulasi R untuk Bali menunjukkan yang semula bulan Mei sempat di bawah 1 dapat berubah menjadi konsisten di atas 1 sepanjang bulan Juni 2020. Perlu respon yang tepat dari berbagai pihak.
Hasil simulasi nilai Ro = 4,79 untuk Indonesia menunjukkan bahwa batas ambang herd immunity adalah 79% pupulasi Indonesia perlu imun. Hal ini hanya layak dilakukan bila ditemukan vaksin yang efektif dan biaya terjangkau.
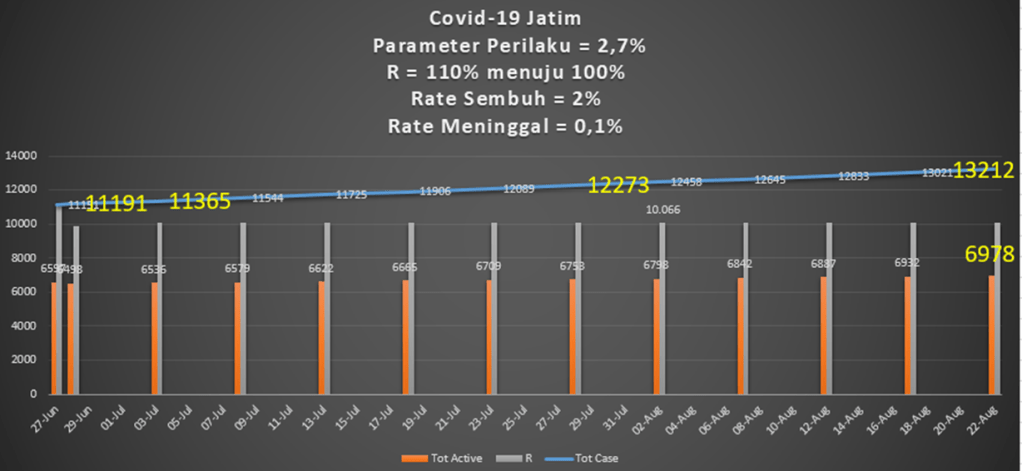
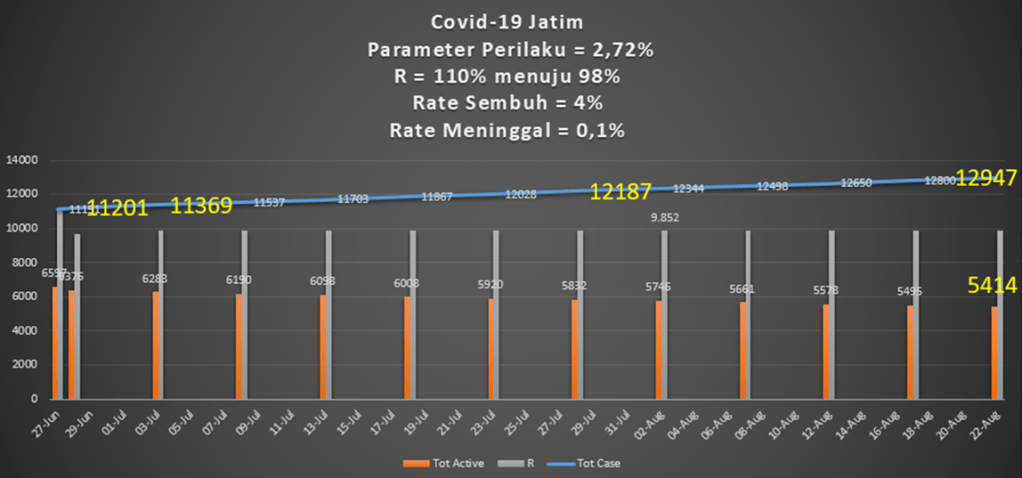
Dari model yang dikembangkan, nilai R mendapat feedback posistif dari parameter perilaku P. Maka perlu menurunkan nilai parameter P agar nilai R menjadi turun. Sedangkan angka kesembuhan S memberi feedback negatif maka dengan meningkatkan angka kesembuhan makin menurunkan angka R.
Hasil estimasi R dengan GMR, meski barangkali berbeda dengan estimasi metode lain, dapat kita gunakan untuk memprediksi pertumbuhan wabah karena hakikatnya menghitung ratio geometri suatu deret.

Kesimpulan dan Saran Lanjutan

Estimasi nilai R dengan metode GMR terbukti sah secara teori matematika.
Metode GMR berhasil mengestimasi nilai R efektif mau pun nilai Ro.
Proses perhitungan GMR dapat dilakukan dengan mudah menggunakan perangkat komputer sederhana.
Proses yang mudah memungkinkan GMR memberi feedback yang cepat kepada berbagai pihak untuk memberi respon yang tepat terhadap pandemi.
Saran lanjutan adalah perlu dilakukan kajian lebih mendalam metode memperoleh data total kasus aktif yang akurat sehingga memberikan nilai R yang lebih akurat. Perlu juga kajian lanjutan faktor-faktor apa saja yang mempengaruhi nilai R sehingga kita dapat mengendalikan suatu wabah dengan lebih efektif.

Ide untuk Bu Khofifah Turunkan Covid Jatim

Jatim berhasil jadi “juara” covid-19 di akhir Juni 2020. Menyalip DKI Jakarta. Total terinfeksi mencapai 11 ribuan orang lebih. Bu Gubernur Khofifah dikabarkan sedang menyiapkan langkah terakhir untuk menangani corona. Bahkan presiden Jokowi juga sempat mendatangi Jatim agar covid lebih terkendali. Apa bisa?

Semoga bisa. Semoga berhasil.

Berikut beberapa ide hasil simulasi saya. Barangkali Jatim dapat memanfaat model matematika dan simulasi komputer untuk menurunkan pandemi corona Jatim.

Perilaku normal mengantar 25 ribu orang terinfeksi

Dalam 60 hari ke depan, hasil simulasi saya menunjukkan akan ada 25 ribuan orang terjangkit corona di Jatim. Kasus aktif 18 ribuan orang sedang dirawat atau karantina pada akhir Agustus.

Perilaku normal ini adalah dengan skenario perilaku masyarakat mirip dengan sekarang (P = 10,9%) dan angka kesembuhan 2%. Kondisi normal ini akan mempertahan angka reproduksi virus R = 1,10. Tentu saja kondisi seperti ini perlu dicegah dengan berbagai macam usaha yang tepat.

2. Manajemen perilaku sosial berhasil meredakan covid

Perilaku sosial berperan besar dalam penyebaran corona. Maka keberhasilan manajemen perilaku sosial menentukan penurunan angka covid-19 di Jatim. Berhasil menahan total kasus corona di 13 ribuan pada akhir Agustus 2020. Angka R bergerak menuju 1,00.

Termasuk dalam manajemen perilaku adalah disiplin pakai masker, rajin cuci tangan, tracing, dan lain-lain. Agar manajemen perilaku efektif maka kita perlu memanfaatkan kajian data sains. Sehingga hanya perilaku yang berdampak saja yang dicegah. Tidak harus lockdown total.

Seperti kita tahu beberapa negara yang melakukan lockdown total ada yang berhasil meredakan corona dan ada pula yang belum berhasil. Sementara negara yang tidak lockdown total ada yang berhasil dan ada pula yang tidak berhasil.

3. Meningkatkan angka kesembuhan

Meningkatkan angka kesembuhan dua kali lipat dari 2% menjadi 4% berhasil mencegah total kasus menjadi hanya 12 ribuan di akhir Agustus. Skenario ini dikombinasikan dengan manajemen perilaku.

Skenario gabungan ini berhasil menurunkan R = 0,98 dari semula R = 1,10. Kondisi ini tentu saja bagus sekali. Kasus pandemi akan mereda dengan seiring berjalannya waktu.

Semoga Jatim dan umumnya seluruh dunia berhasil menangani corona dengan baik.

Berikut ini adalah model matematika dan sistem dinamik yang saya gunakan untuk menghitung dan simulasi.

Pergerakan nilai R Jatim berikut ini. (Klik gambar untuk update terbaru.)

Bagaimana menurut Anda?

Metode Eksak Menghitung R0 – Rt- Re

Saya mengembangkan berbagai macam cara menghitung reproduction number R. Awalnya saya mengestimasi Rt dengan geometric mean. Lalu mengembangkan cara estimasi Ro. Dan menyususn sistem dinamik.

Cara menghitung nilai R secara eksak adalah,

Contoh dan bukti keabsahan formula di atas sudah saya tuliskan pada tulisan-tulisan saya sebelumnya.

Kali ini saya akan membahas ulang dengan notasi alternatif. Semoga lebih sederhana. Berlaku lebih luas.

R = reproduction number = Rt = Re = Reproduction effective
a[n] = banyaknya total kasus aktif pada waktu ke n.
I = periode inkubasi, misal mean I untuk covid-19 = 5 hari

Metode yang kita bahas ini adalah metode eksak. Dalam arti kita masih memandang sistem sebagai deterministik. Sedangkan di alam ini hampir semua kasus ada ketidakpastian. Maka lebih mirip dengan sistem stokastik dan kita perlu memanfaatkan statistik.

a[h] = S[h] – S[h – K]
a[h – I] = S[h – I] – S[h – I – K]

maka

h = hari ke h
K = periode kasus keluar, kasus selesai, misal untuk covid adalah 9 hari

S[h] = jumlah kasus aktif baru dari hari ke 1 sampai hari ke h.

S[h] = u[1] + u[2] + … + u[h]
u[h] : banyaknya kasus aktif baru pada hari ke h.

Maka

a[h] = S[h] – S[h-K] = u[h] + u[h-1] + … + u[h-K+1]

a[h-I] = S[h-I] – S[h-I-K] = u[h-I] + u[h-I-1] + u[h-I-K+1]

Perhatikan bahwa masing-masing suku deret di atas adalah r^I kali dari masing-masing suku deret di bawah. Maka perbandingannya,

Untuk contoh corona karena I = 5 hari maka

Di mana r adalah rasio pertumbuhan harian total kasus aktif. Metode ini sah ketika h > 2I.

Jika h < 2I

maka kita memperoleh nilai

R transien = R[T]

Formula yang sama masih bisa kita gunakan dengan definisi tambahan.

a[h] = a[1] untuk semua h < 1

Kadang kita juga bisa menganggap a[h] = 0 untuk memudahkan analisis dengan hasil yang tetap akurat.

Rp = R puncak = Nilai maksimum dari R[T].

Bisa ditunjukkan R[T] yang lain adalah lebih kecil atau sama dengan Rp. Anggap a[h] = 0 untuk h < 1.

Terbukti R[T] lebih kecil dari Rp.

Selanjutnya kita bisa memanfaatkan Rp untuk menentukan Ro. Karena Rp terjadi di masa-masa penularan maka nilai Rp berhubungan dengan nilai puncak R yaitu R0.

Dengan memecahkan persamaan

maka

Sedangkan nilai R[T] sebelum Rp pasti lebih kecil dari Rp karena pembilang lebih kecil, yaitu banyaknya suku kurang dari I suku.

Yang menarik juga bahwa R[T] = R[n], membentuk fungsi kontinyu R ketika n = 2I.

Bagaimana menurut Anda?

Indonesia Melejit Vs Jabar Goyang: Covid-19

Kita makin seru saja menghadapi corona. Presiden mengunjungi Jatim untuk memastikan Jatim landai dalam 2 pekan ke depan. Kang Emil menghentikan PSBB Jabar. Roda ekonomi diharapkan bergulir dan masyarakat tetap aman.

Jabar termasuk cukup baik, kondisi saat ini, dibanding Jatim.

Jabar bergoyang nilai reproduksi virus di bawah 1 dan kadang menyentuh 1 atau melewati. Goyangan yang tidak buruk. Sedangkan Jatim melejit bahkan mengalahkan Ibukota Jakarta.

Secara nasional, Indonesia juga konsisten melejit dengan nilai R di atas 1.

Saya pernah bersyukur karena R sudah turun dari 1,16 ke 1,14 waktu itu. Tapi dikomplain teman saya. Katanya, berita luar negeri menyatakan sebaliknya, wabah di Indonesia masih terus meningkat.

Saya jawab: saya memakai bahasa yang halus. Meski R turun ke 1,14 tapi masih di atas 1 artinya wabah memang masih menular.

R Indonesia masih konsisten di atas 1 maka perlu kolaborasi apiq antara seluruh anak negeri.

Saya berharap para pemimpin memiliki data akurat nilai R setiap saat. Sehingga ketika memberikan arahan dapat memonitor dampaknya terhadap wabah. Bila suatu kebijakan menyebabkan R turun maka lanjutkan. Bila menyebabkan R naik maka revisi segera.

2. Jabar bergoyang di bawah dan atas 1 nilai R terakhir ini.

Grafik warna kuning (orange) bergoyang naik turun. Itulah banyaknya kasus aktif di Jabar. Bisa turun sampai 1200an orang. Lalu naik lagi maksimal mendekati 1400an. Bergoyang terus selama R juga bergoyang di sekitar 1.

Kapan berakhir? Tidak akan berakhir – kecuali R konsisten di bawah 1.

Total orang yang terinfeksi tentu terus naik seperti grafik berwarna merah. Total mencapai 23 ribu lebih dalam 10 bulan ke depan.

Bagaimana dampak dihentikan PSBB di Jabar? Tidak masalah!

Selama R di bawah 1 maka grafik akan turun. Pandemi corona akan mereda seiring waktu.

3. Pentingnya data R yang akurat setiap saat.

Saya berpikir kita perlu data R yang akurat misal tiap jam. Sehingga para pengambil kebijakan dapat bersikap dengan cepat. Kita bisa merancangnya. Tidak mudah tapi bisa. Semoga banyak bermanfaat!

Catatan:
Kondisi Jatim mirip nasional dan Jabar mirip Jakarta.

Bagaimana menurut Anda?

Pesan Buat Kang Emil: Jabar Masih Naik Turun

Angka reproduksi Jawa Barat masih naik turun. Kadang R masih di atas 1, masih mewabah. Kadang R di bawah 1, virus mereda.

Tapi Kang Emil, Bapak Gubernur Jabar dapat info bahwa R Jabar sudah di bawah 1 selama 6 minggu terakhir.

“Kang Emil mengatakan, keputusan dihentikannya PSBB itu berdasarkan pada angka reproduksi virus yang terus bertahan di bawah 1 selama 6 minggu terakhir.” Sumber detik.com .

Keputusan menghentikan PSBB atau melanjutkan PSBB adalah wewenang beliau yang berwenang. Sebagai rakyat kita mendukung apa pun keputusan terbaik para pemimpin. Tetapi jika salah data atau salah analisis maka perlu data pembanding.

Saya sendiri siap memberikan analisis pembanding nilai R untuk Jabar dan wilayah Indonesia lainnya. Saya rutin menghitung angka R tiap hari dan berbagi melalui web pamanapiq.com/covid . Dengan data dan analisis pembanding ini semoga Jabar lebih baik dalam mengambil keputusan. Semua warga aman, sehat, selamat, dan roda ekonomi makin maju.

R Jabar lebih banyak di atas 1 – waspada

Kisaran 6 Juni sampai dengan 12 Juni nilai R Jabar pernah di bawah 1. Tapi selain itu, sebagian besar di atas 1. Akhir Mei sampai 6 Juni di atas 1. Dan 12 Juni sampai 15 Juni juga di atas 1. Bahkan terakhir 25 Juni R = 1,078.

2. Jabar masih merah – versi Bonza

Bonza memberikan analisis pembanding untuk provinsi di Indonesia.

Warna merah, saya lihat Jumar, 26 Juni 2020, menandakan Jabar masih di atas 1 nilai R nya. Sehingga masih waspada dengan virus yang terus berkembang.

3. Nilai R = 1,12 pada 18 Juni 2020

Masih dari Bonza, menyebutkan nilai R = 1,12. Tentu kita perlu lebih waspada dengan data dan analisis tersebut.

Bagaimana pun itu semua adalah sekedar data dan analisis pembanding yang barangkali beguna untuk menjadi pertimbangan dalam mengambil kebijakan yang berkaitan dengan kepentingan umum.

Semoga bermanfaat…!

Bagaimana menurut Anda?

Terima kasih.

Metode Eksak Menghitung Ro – Geometric Mean

Nilai Ro adalah nilai maksimum dari Rt atau Re = reproduction effective.

Maka kita menduga nilai Ro terkait dengan puncak-puncak grafik dari R terhadap waktu.

Kita sudah buktikan untuk h > K dan h > I nilai R kita hitung dengan perbandingan geometri total kasus aktif sebagaimana berikut ini.

Selanjutnya kita akan menyelidiki kasus di mana h <2I dan khususnya I <= K. Untuk mendapatkan estimasi nilai Ro. (Untuk I > K kita sudah mendapat nilai R sejak h > I).

Misalkan a[n] adalah jumlah total kasus aktif pada waktu n, dan r adalah rasio geometri harian.

bahwa nilai Rp di atas lebih besar dari semua nilai R lain. Misal bila kita geser 1 suku ke kanan,

Terbukti Rp > R.

Faktor pengali r/(r+1) selalu kurang dari 1 karena r bilangan positif atau 0. Jadi R < Rp. Demikian juga bila suku-suku deret digeser 2 suku atau lebih ke kanan.

Bahkan jika kita menggeser sampai n suku ke kanan kita peroleh,

Hasil ini konsisten dengan formula awal ketika h > I.

Sedangkan menggeser a[n + 1] ke kiri mengakibatkan pembagian a[n] oleh a[0]. Di mana kita belum memperoleh data a[0] sehingga kita definisikan sebagai R = 1. Seberapa jauh pun kita menggeser ke kiri maka kita definisikan konstan R = 1.

Dengan mengambil n = I maka kita mendapatkan Ro dengan memecahkan persamaan yang berhubungan dengan Rp.

Rp adalah nilai R pada puncak grafik, bukan nilai Ro sebenarnya. Tetapi nilai Ro adalah justru r^n = r^I. Maka dengan memecahkan persamaan Rp kita peroleh r^I = Ro.

Contoh 1:
r = 2
n = I = 3 hari
K = 3 hari

Maka:
a[n+1] = a[3+1] = 1 + 2 + 4 + 8 – 1 = 14
a[1] = 1

Rp = 14 = {(2^4 – 1)/(2 – 1)} – 1 = 15 – 1 = 14 … … … (benar).

Atau

Rp = 14 = (r^4 – 1)/(r – 1) – 1

Maka kita selesaikan persamaan di atas kita peroleh r = 2. Dan Ro = r^3 = 2^3 = 8.

Contoh 2:
r = 2
n = I = 2 hari
K = 2 hari

Maka:
a[n+1] = a[2+1] = 1 + 2 + 4 – 1 = 6
a[1] = 1

Rp = 6 = {(2^3 – 1)/(2 – 1)} – 1 = 7 – 1 = 6 … … … (benar).

Atau

Rp = 6 = (r^3 – 1)/(r – 1) – 1

Pilih solusi positif r = 2.

Maka kita selesaikan persamaan di atas kita peroleh r = 2. Dan Ro = r^n = 2^2 = 4.

Cara Praktis Menentukan Ro dari Grafik

Buat grafik fungsi R terhadap waktu.
Tentukan puncak grafik = Rp.
Tentukan n = I
Pecahkan persamaan Rp dan r seperti di atas.
Maka Ro = r^n = r^I.

Selesai.

Proses statistik/stokastik

Metode eksak menentukan Ro sudah kita uraikan di atas. Pada kenyataannya kita lebih sering menghadapi sistem stokastik yang melibatkan perhitungan statistik lengkap dengan ketidakpastiannya.

Maka kita dapat menentukan nilai Ro dengan pendekatan statistik. Di mana,

I = periode inkubasi = mean dari periode inkubasi = 2 hari untuk covid

K = periode keluar = mean dari periode keluar = 10 hari, misalnya, untuk covid-19.

Misal dari grafik R covid suatu wilayah kita peroleh Rp = 5. Maka

Kesimpulan: Ro = 1,7913^2 = 3,21

Kita coba contoh lagi.

Misal untuk grafik R covid diperoleh Rp = 20 dengan I = 5.

Kesimpulan Ro = 1,50439^5 = 7,71.

Wow… hebat juga!?

Bagaimana menurut Anda?

Awal Mula Akhir Pandemi Covid-19

Awal pandemi dimulai dari pasar hewan Wuhan, Cina. Lalu menyebar ke seluruh dunia. Belum ada bukti kuat tentang itu. Tapi bukti untuk yang lain lebih tidak kuat lagi.

Kali ini kita akan membahas bagaimana dari 1 orang yang terinfeksi bisa menginfeksi 9 juta orang lebih di seluruh dunia pada akhir Juni 2020 ini.

Kasus awal,

A[n-1] = 1
R = 1
S = 0 = D
P = 0

Ketika ada 1 orang terjangkit, orang ini awalnya tidak bisa menulari siapa pun. R = 1 dan hanya dirinya sendiri yang aktif sebagai terjangkit. P = 0 maka tidak ada tambahan orang terjangkit, meski dikali R. Demikian juga tidak ada yang sembu (S = 0) dan tidak ada yang mati (D = 0).

Kondisi awal seperti di atas bisa saja setimbang dalam beberapa waktu. Bila, misal, ada 1 yang tertular maka kesetimbangan akan berubah.

P = 0 berubah menjadi P = 1

R*P = 1*1 = 1

A[n] = A[n-1](1 + R*P – S – D) = 1 (1 + 1 – 0 – 0) = 2

R = A[n] / A[n – 1] = 2/1 = 2

Satuan dari n bisa harian, mingguan, atau lainnya. Sementara kita abaikan dulu. Atau anggap saja 1 harian.

Anggap aktif 2 orang ini bertahan beberapa waktu. Artinya tidak ada tambahan kasus baru. Padahal R = 2. Tapi karena P = 0 maka tidak ada penularan.

A[n] = A[n-1](1 + R*P – S – D) = 2 (1 + 0 – 0 – 0 )= 2

R = A[n] / A[n – 1] = 2/2 = 1

Dan kembali R = 1. Virus tidak jadi menyebar.

Bila perilaku masyarakat begitu terbuka. Sering berkumpul. Maka droplet bisa menyebar kemana-mana. Kita bisa memisalkan dengan P = 1. Selanjutnya kita lihat perkembangan kasus.

A[n] = A[n-1](1 + R*P – S – D) = 2 (1 + 1*1 – 0 – 0) = 4

R = A[n] / A[n – 1] = 4/2 = 2

Dan berkembang terus menjadi wabah misal jadi ada orang aktif 6 000 orang.

A[n] = A[n-1](1 + R*P – S – D) = 6000(1 + (2)*(1) – 0 – 0) = 18 000

R = A[n] / A[n – 1] = 18000/6000 = 3

Kita lihat begitu cepat virus menyebar menjadi pandemi. Sebesar apa pun pandemi maka akan tetap ada akhirnya. Herd Immunity (HI) adalah salah satu bentuk akhir pandemi.

Herd Immunity

HI terjadi ketika P menjadi 0. Mungkin karena sudah ditemukan vaksin. Atau hampir seluruh populasi sudah pernah terinfeksi maka jadi imun. Atau ada cara lain menjadi imun.

Misal sudah ada 6 juta orang aktif. Dan R = 2 tapi P menuju 0.

A[n] = A[n-1](1 + R*P – S – D) = 6(1 + 2*0 – 0 – 0) = 6

R = A[n] / A[n – 1] = 6/6 = 1

Semula R = 2 berikutnya berubah jadi R = 1.

Bila ada yang sembuh atau meninggal maka jumlah aktif berkurang. Maka R turun ke bawah 1. Terbentuklah HI. Yaitu 6 juta orang aktif terinfeksi ini akan bertahan beberapa waktu. Atau jumlah mereka berkurang karena sembuh atau lainnya. Dan tidak ada perkembangan wabah. Pandemi berakhir.

Analisis di atas juga bisa kita lakukan dengan berfokus pada menghitung R.

Nilai R = 1 pada awalnya akan betambah dengan bertambahnya nilai P. Sehingga terjadi wabah. Tetapi P pada akhirnya mengecil jadi 0 maka R turun ke 1. Terbentuk HI. Dan menjadi di bawah 1 karena ada yang sembuh atau meninggal. Pandemi berakhir.

Bagaimana menurut Anda?

Anti Lockdown: Solusi Pandemi Covid-19

Wuhan di Cina berhasil mengendalikan pandemi corona dengan lockdown. Sedangkan negara lain ada yang kalang kabut justru karena lockdown. Swedia dianggap berhasil menghadapi pandemi covid-19 tanpa lockdown. Bagaimana dengan Indonesia?

Indonesia bisa membuat pandemi reda tanpa lockdown dengan meningkatkan rate kesembuhan menjadi 27%. Bahkan cukup 24% maka pandemi mulai mereda.

Terlihat dari grafik di atas total kasus aktif makin mereda jadi 4 ribuan di 60 hari ke depan. Dan nilai R turun di bawah 1.

Saya menggunakan model matematika Repcon – Reproduction Number Controlling – untuk membuat analisis di atas. Di mana R dapat kita formulasikan dengan diagram blok berikut.

R[n] = 1 + P*R[n-1] – S – D

Sedangkan total kasus aktif kita modelkan berikut.

A[n] = (1 + R[n-1]*P – S – D) A[n-1]

2. Indonesia dapat meredakan pandemi dengan “mengendalikan” perilaku sosial. Cukup menurunkan parameter perilaku menjadi p = 0,065 maka pandemi mereda dalam 60 hari ke depan.

Kita perhatikan dari grafik, total kasus aktif turun menjadi 10 ribuan orang pada 60 hari ke depan. Dan tentu saja R juga turun di bawah 1.

Banyak orang menganggap bahwa parameter perilaku ini hanya bisa dikendalikan dengan lockdown. Tetapi tidak ada hubungan pasti di antara keduanya. Kita justru perlu mencari tahu perilaku apa saja yang efektif bisa menurunkan parameter perilaku.

Diagram blok di atas baru usulan awal dari saya. Perlu kajian lebih mendalam. Saya kita peran data sains sangat penting untuk ini.

3. Pandemi Indonesia tidak akan mereda bila R dibiarkan di atas 1 secara konsisten.

Tanpa usaha serius maka pandemi benar-benar menjadi pertumbuhan eksponensial. Baik dari sisi total kasus aktif, total terinfeksi, total meninggal, dan lain-lain. Tentu saja hal ini harus dicegah.

Dengan kajian yang mendalam dan tepat, saya yakin Indonesia mampu meredakan pandemi corona.

Bagaimana menurut Anda?

Prediksi Covid di Indonesia: 23 Juni – 22 Agustus 2020

Pada 22 Agustus 2020 kasus corona covid-19 di Indonesia makin berkembang. Estimasi ada 257 ribuan total orang terinfeksi dan 149 ribuan orang di antaranya masih kasus aktif. Perlu dirawat atau isolasi mandiri.

Apakah hasil prediksi semacam itu tampak baik-baik saja? Atau harus lebih waspada?

Saya meprediksi berdasarkan data resmi sampai 23 Juni 2020. Bila ditambahkan estimasi “laporan tidak resmi” barangkali hasil prediksi akan lebih pesimis. Saya menggunakan pemodelan matematika covid-19: reproduction number controlling. Saya singkat sebagai repcon.

Metode repcon mengestimasi nilai R = 1,10 dan parameter perilaku percepatan penyebaran p = 23%. Di mana 23% ini mengindikasikan bahwa masyarakat Indonesia menyebarkan corona 23% lebih banyak dari periode sebelumnya.

Makin besar nilai p maka virus makin menyebar. Makin kecil virus makin tertahan. Disiplin pakai masker, jaga jarak, dan cuci tangan diyakini bisa menurunkan nilai p.

Sementara rate sembuh S = 12% dan rate death D = 1%. Makin besar yang sembuh maka virus makin sulit berkembang. Angka 12% menunjukkan bahwa 12% orang yang aktif akan sembuh.

Sedang rate meniggal 1% perlu diwaspadai. Karena pada tanggal 22 Agustus diperkirakan akan ada yang meninggal 1% x 128 ribu = 1280 orang.

Sampai akhir Agustus nilai R masih di atas 1 kisaran 1,16. Menunjukkan pandemi belum berakhir.

Untuk menurunkan R bisa dengan memperkecil paramater perilaku p dan memperbesar rate sembuh S.

Bagaimana menurut Anda?

Pemodelan Matematika Covid-19: Reproduction Number Controlling

Mengendalikan angka R menjadi salah satu strategi untuk meredakan pandemi corona. Reproduction number, R, lebih dari 1 maka wabah masih bertambah. Sedangkan bila R kurang dari 1 maka wabah mulai mereda.

Grafik di atas aalah kondisi Indonesia akhir Juni 2020 dengan R = 1,16. Dengan menetapkan parameter percepatan p = 0,13 maka R secara pelan turun dan stabil di R = 1 dalam 60 hari. Total aktif konstan sekitar 25 ribuan.

Tetapi grafik di bawah lebih mendekati kondisi Indonesia sebenarnya di mana R sekitar 1,16 dan 1,17. Total aktif menjadi 173 ribu lebih, dalam 60 hari ke depan. Dan total kasus lebih dari 304 ribu orang. Tampaknya kondisi ini terlalu riskan.

Skenario yang lebih baik dapat dengan menurunkan P = 0,065 atau meningkatkan rate sembuh menjadi 24%.

Dengan menurunkan parameter percepatan = 0,065 artinya kita mempersulit virus menyebar. Misal mengenakan masker lebih disiplin. Kita lihat dari grafik di atas, total kasus aktif menurun tinggal 10 ribuan orang setelah 60 hari. Maka R turun di bawah 1 dan wabah mereda di Indonesia.

Strategi alternatif yang bisa dilakukan adalah dengan menambah rate sembuh jadi 24% dari yang semula 12% (terhadap total aktif). Dengan mendukung lebih kuat penangan kesehatan maka kesembuhan diharapkan lebih tinggi.

Kita lihat dari grafik di atas, total kasus aktif lebih cepat turun dan hanya tinggal 4 ribuan orang setelah 60 hari ke depan. Tentu R sudah turun di bawah 1 dan pandemi corona mereda di Indonesia.

Bagaimana menurut Anda?

Model Dasar